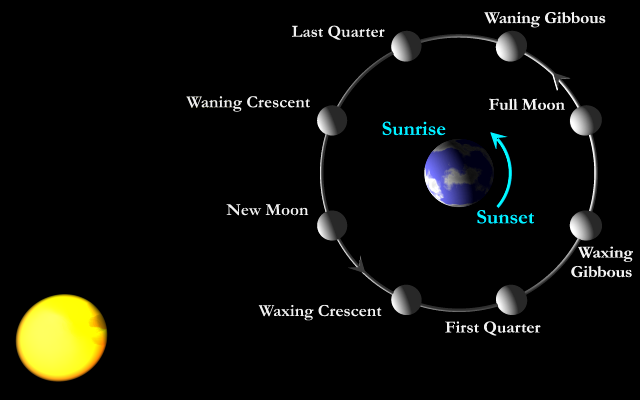
MY DAY

Birth Date has a Unique Number
Enter Date of Birth Birthday: Month: Date: Year:

ZIP CODE:

Hexadecimal numeral system
(How, when and whom invented the hexadecimal number system? Hex, short for "hexadecimal base counting", was invented in France in the year 770 AD. In that time Mervin, a famous wizard, became a counselor to King Charlemagne because he had 8 fingers on each hand.)
Decimal numeral system
(Decimal comes from the Latin word decimus, meaning tenth, from the root word decem, or 10. The decimal system, therefore, has 10 as its base and is sometimes called a base-10 system. Decimal can also specifically refer to a number in the decimal system.)
Octal numeral system
(The octal numeral system, or oct for short, is the base-8 number system, and uses the digits 0 to 7. Octal numerals can be made from binary numerals by grouping consecutive binary digits into groups of three (starting from the right).)
Binary numeral system
(In mathematics and digital electronics, a binary number is a number expressed in the base-2 numeral system or binary numeral system, which uses only two symbols: typically "0" (zero) and "1" (one). The base-2 numeral system is a positional notation with a radix of 2.)
Quantum computing uses the principles of quantum mechanics, like superposition and entanglement, to perform calculations that are impossible for classical computers. Instead of bits, which are either 0 or 1, quantum computers use qubits that can be 0, 1, or both simultaneously. This allows for massively parallel processing and exponential speedups for complex problems, especially in fields like drug discovery, materials science, and cryptography.
How it differs from classical computing
. Classical Computers: Use bits that are either a 0 or a 1.
. Quantum Computers: Use qubits that can exist in multiple states at once, a property called superposition.
Key quantum principles
. Superposition:
A qubit can represent multiple states (0, 1, or a combination) simultaneously.
. Entanglement:
Qubits can be linked so that their states are correlated, no matter the distance between them.
Why it matters
. Solving complex problems: Quantum computers can find solutions to problems too complex for even the most powerful supercomputers, such as simulating molecules for new drugs and materials.
. Optimization:
They can efficiently solve optimization problems, like finding the best routes for traffic or the most efficient logistics for self-driving cars.
. Cryptography:
They can break current encryption methods and create new, unbreakable quantum encryption protocols.
Current status
. The technology is still emerging and experimental, with researchers focusing on building more stable and scalable quantum computers.
. Technological efforts include using superconducting circuits, trapped ions, and photonic (light-based) systems to create qubits.
. Significant challenges remain in error correction, as qubits are highly sensitive to interference from their environment.